[백준] 파이썬 17396 - 다익스트라와 1e9

1. 문제 발견

https://www.acmicpc.net/problem/17396

 

오래간만에 다익스트라 알고리즘을 연습하기 위해 푼 문제이다.

문제를 풀 때 습관적으로 초기 가중치 값을 1e9로 하고 푸니 틀리게 되었다.

 

https://www.acmicpc.net/board/view/153011

질문 게시판을 보니 이 문제에서는 가중치가 1e9 이상 갈 수 있다고 한다.

 

2. 문제 분석

문제에서 정점의 수는 최대 100,000개, 간선의 수는 최대 300,000개, 간선 가중치는 최대 100,000으로 주어졌다.

최단 경로의 가중치가 최대로 나올 수 있는 그래프는 다음과 같은 형태의 그래프일 것이다.

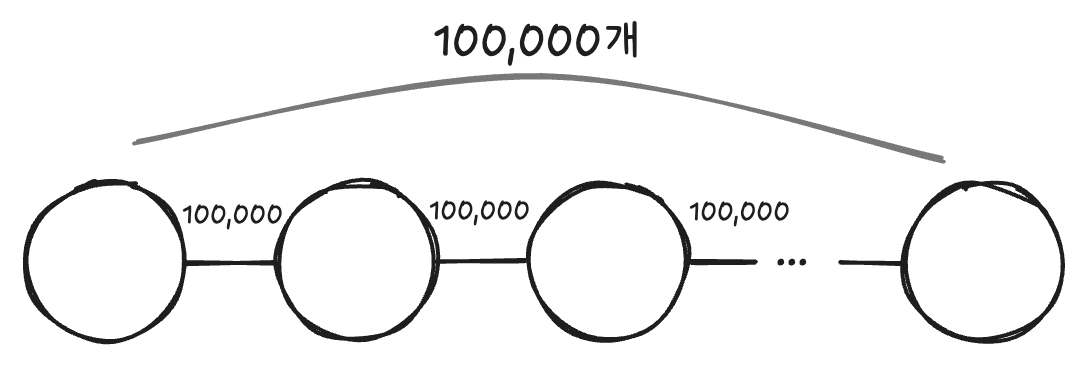
위 그래프의 최단 거리 가중치를 나이브하게 계산해 보면 100,000 * 100,000 = 10,000,000,000 (100억)이다.

내가 사용한 가중치인 1e9는 10억이므로 충분히 넘는 숫자다.

3. 문제 해결

# before
dist = [1e9] * (N + 1)

# after
dist = [float('inf')] * (N + 1)

파이썬에서는 float('inf')로 양의 무한대를 표현할 수 있다.

최대값을 표현할 때는 안전하게 float('inf')를 사용해야겠다.

4. 코드

import sys
from collections import defaultdict
import heapq

input = sys.stdin.readline

N, M = map(int, input().split())
visible = [*map(int, input().split())]
graph = defaultdict(list)
for _ in range(M):
    a, b, t = map(int, input().split())
    graph[a].append((b, t))
    graph[b].append((a, t))

MAX = float("inf")

def dijkstra():
    hq = []
    heapq.heappush(hq, (0, 0))

    dist = [MAX if v == 0 else 0 for v in visible]
    dist[-1] = MAX
    
    while hq:
        w, n = heapq.heappop(hq)
        
        if w > dist[n]:
            continue
        
        for nxt, nxt_w in graph[n]:
            if dist[nxt] > w + nxt_w:
                dist[nxt] = w + nxt_w
                heapq.heappush(hq, (w + nxt_w, nxt))
                
        
    return dist[-1] if dist[-1] != MAX else -1

res = dijkstra()
print(res)